Szimmetria – aszimmetria

Gyakran tapasztaljuk, hogy a szimmetrikus látványt szebbnek találjuk. Ez azonban nem zárja ki, hogy olykor az aszimmetrikus arányokat is tetsszenek. Egy növény levelének vagy magjának spirális elrendeződése, vagy egy kép aranymetszés pontjának kiugrása ugyanúgy élményt jelenthet, holott ezeknél az arányok aszimmetrikusak. De mit is jelentenek valójában ezek a fogalmak, és hol találkozhatunk velük?

Definíció, helyesírás

A szimmetria a tudomány meghatározása szerint egy rendszernek egy olyan tulajdonsága, amely változatlan marad a rajta elvégzett műveletek során. Egyszerűbb megfogalmazásban a szimmetria azt jelenti, hogy valaminek egyformák az elemei, és ezek tükörképszerűen állnak egymással szemben.

A szó a görög szün = együtt, össze és a metró = mér kifejezések összetételéből, a szümmetriából származik. (Első tagjának, a „szün”-nek a magyarhoz igazított változataival egyébként még a jól ismert „szimfónia”, „szinopszis”, „szinkron”, „szinkópa” és számos, további szin- vagy szim- kezdetű szóban is találkozunk.) Az aszimmetria, vagyis a „szimmetriátlan” jelentésű szó pedig ennek az a- fosztóképzővel ellátott változata.

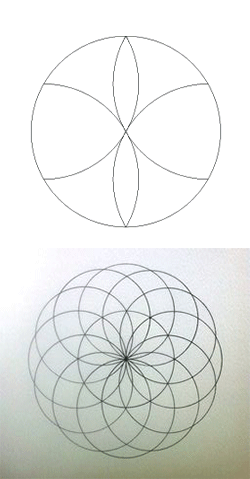Az első, szimmetrián alapuló díszítések egyike az az alapminta volt, amelyet körzővel rajzoltak meg. Ehhez arra kellett figyelni, hogy a rajzoló nagyon pontosan szúrja le a körző hegyét a kör vonalán a megfelelő helyre. Majd miután már rutinná váltak az efféle megoldások térhatású rajzokat is létrehoztak ezen az egyszerű módon. (Kép forrása)

Ez egyébként az egyik leggyakrabban hibásan írt szavunk, amelyet sokan hajlamosak két Sz-szel és egy M-mel mondani és írni („asszimetria”). Ennek az lehet az oka, hogy a magyarban a szavak elölhangsúlyosak, amit azonban itt mintha meg akarna törni a második-harmadik szótagba kerülő két M. Ezért sokan önkéntelenül úgy nyomják meg az első szótagot, hogy ott is megkettőzik a mássalhangzót.

Aszimmetriával a leggyakrabban a természetben és a művészetben találkozunk. A természetben a növények igen gyakran mutatják ezt az arányosságot: kevés kivételtől eltekintve például a fák ágai is aszimmetrikusan nőnek. Bonyolultabb módon azonosíthatjuk be az aszimmetriát az olyan növényeknél, amelyeken a levelek vagy a pikkelyek csigavonalban, vagyis egy spirálisban vannak jelen. Itt az aszimmetria törvényszerűségeit a matematika segítségével tudjuk kimutatni. Ha például egy tobozon megszámoljuk a pikkelyek egy-egy sorát, akkor azt kapjuk, hogy a középpontból kiinduló vonalak végül egy olyan zárt rendszerré állnak össze, amelyben a spirálisok száma mindig az ún. Fibonacci-sor értékeihez vezet. Ez pedig azt jelenti, hogy az összkép az aranymetszés arányait tartalmazza. Az aszimmetriának pedig az aranymetszés a legkarakteresebb kifejezője. (Részletesen lásd a spirálról szóló cikkünkben is.)

Szimmetria a természetben és a mesterséges világban

A kétféle arányosság közül a leggyakrabban a szimmetriával találkozunk.

Az egyik leglátványosabban szimmetrikus síkidom a négyzet. Ennek szimmetriáját azzal tudjuk a legjobban érzékeltetni, hogy berajzolunk a középvonalán át egy egyenest. Ez egyértelművé teszi, hogy a vonaltól jobbra és balra látható részek egyformák. Ha pedig a négyzetet 90 fokkal elfordítjuk, ez a művelet szintén mit sem fog változtatni azon, hogy az idom egyes részei ugyanolyanoknak látszódjanak. A szimmetriának tehát fontos eleme az a tengely, amely megmutatja a szerkezet lényegét.   

A képi szimmetriával a természetben, és annak részeiként a saját testünkön is találkozhatunk, hiszen ha a testünk közepén húzunk egy képzeletbeli vonalat, akkor az ugyanúgy két, azonos formájú részre vág minket. Igaz, a megfelelések soha nem tökéletesek: akár az arcunkon, akár a kezünkön-lábunkon nézzük meg közelebbről is a részleteket, azt fogjuk látni, hogy elég sok eltérés lehetséges.

Nem ritka, hogy valakinek az egyik szeme láthatóan kisebb, mint a másik (sőt, még olyasmi is előfordulhat, hogy az egyik szeme kék, a másik barna, ami ugyan nem az elrendezést töri meg, de a látvány egységét mindenképpen). Az ember szájának vonala is állhat másképp az arca jobb felén-balfelén, és azt is mindenki ismeri a cipőbolti vásárlásaiból, hogy többnyire a lábfejünk sem egyforma méretű. Ugyanígy a hajunk is lehet szabálytalan elrendezésű, amit a benne lévő, ún. forgók jeleznek. Mindezektől függetlenül az emberi test kívülről nézve alapvetően szimmetrikus elrendezésű. De a természet más területein is gyakran látunk egyértelműen és szabályosan ismétlődő, egybevágó formákat.

Még a szervetlen világban is: a kristályoknak például kiemelkedő szerkezeti jellemzőjük lehet a szimmetria. (A kristálytanban a szimmetriát arra is felhasználják, hogy ennek eszközével csoportosítsák a kristályokat fölépítő atomi és molekuláris szerveződéseket, illetve osztályozzák a lehetőségek készletét.)

Ugyanígy az ember által teremtett világban is léteznek azonos tulajdonságú elemek, amelyeket nagyobb rendszerekké lehet összekapcsolni, vagyis a mesterséges szimmetria is jelen van az életünkben. Ebből adódik, hogy a szimmetria több szakterület, illetve tudományág fogalmi készletének is a része.

Dürer 1500 és 1505 között készítette az ún. Paumgartner oltárt, amely egy hármasoltár, más néven triptichon. A triptichonok három részből álló, táblára festett képegyüttesek voltak, illetve olyan oltárszekrények, amelyeknek a két oldalán lévő keskenyebb szárnyakat be lehetett hajtani. Ezek a középkortól rendkívül népszerű, szimmetrikus szerkezetű bútorok voltak a templomokban. Dürer alkotásának érdekessége, hogy miközben az egész kompozíció szimmetriát mutat, a középső képen, amelyen Jézus születését látjuk, a Máriát és a kisdedet védő párkány gerendája éppen a kép aszimmetrikus tengelyén, vagyis az aranymetszés-vonalán fut le a talajig. Az oltár onnan kapta a nevét, hogy a két kihajtható szárnyon egy nevezetes nürnbergi patrícius család két tagját, a Paumgartner fivéreket látni, Szent György és Szent Eustachius képében. Ez Dürer korának jellemző ritter-, vagyis lovagábrázolása volt. (Kép forrása)

A tükrözéses elrendezési formával az ókorban elsősorban a matematikában-geometriában foglalkoztak, és természetesen a gyakorlatban is hasznosították a törvényszerűségeit. A görög Thalész, Pitagorasz, Eukleidész vagy Archimédész geometriájából, illetve matematikájából ugyanúgy nem hiányozhatott a fogalma, ahogyan a legismertebb római építész és hadmérnök, Vitruvius életművéből sem.

Euklidész például háromféle szimmetriát különböztetett meg, az általa leírt, háromdimenziós geometriában:

 1. Középpontos, vagy centrális szimmetriát, amelyet egy pont határoz meg. Ez térbeli, síkbeli és “egyenesbeli” is lehet.

 2. Tengelyes szimmetriát, amelyet egy egyenes határoz meg. (Ez az egyenes a szimmetria tengelye.)  A tengelyszimmetria egyaránt lehet síkbeli és térbeli.

 3. Síkszimmetriát, amely egy síkkal van meghatározva. Ez csak térbeli lehet.

A matematikában a szimmetria olyan, speciális értelmezéseként jelenik meg, amelyet megehetősen sokféle módon és variációban alkalmaznak, a számokra és azok egymáshoz való viszonyaira nézve. Néhány példa: szimmetrikus az a szám, amelynek számjegyeit fordított sorrendben írva ugyanazt a számot kapjuk. Vagy: szimmetrikus mátrix az olyan négyzetes mátrix, amely egyenlő a transzponáltjával (vagyis a sorainak és oszlopainak felcserélésével létrehozott mátrixszal).

Vitruvius vízvezetéket és hajítófegyvereket is tervezett, s ezek mellett egy bazilikát is épített. Ezek mindegyikénél tudatosan használta ki a szimmetria lehetőségeit. Életműve nagy hatást gyakorolt a reneszánsz kori Leonardo da Vincire, aki például az emberi test arányainak tanulmányozása közben szintén nagyon tudatosan fordult a szimmetria jelensége felé. (Részletesen lásd itt.) Őt megelőzően egyébként a magyar származású, bajor festő, Albrecht Dürer (1471-1528) foglalkozott kiemelten a szimmetriával. 

Tárgyak és díszítések

A tárgyak, festmények vagy épületek mellett a leggyakrabban a díszítőművészetben találkozunk a szimmetriával. A szimmetria legegyszerűbb megjelenési formája a díszítősor, amely minden nép művészetében ugyanúgy jelen van, ahogyan később a tömeges ruhagyártásban is elterjedt.

A szimmetrikus elemekből álló, díszítési stílust gyakran a mesteremberek által használt eszközök inspirálták. A népi bútorkészítés díszítésében például hosszú ideig főszerepet játszott az ácskörző, amellyel egyszerűbb és bonyolultabb virágminták hosszú sorát hozták létre. A minták formáját az döntötte el, hogy a megrajzolása során hányszor és hová szúrták le a körző tűjét. (Ha te is szeretnél körzővel készített mintákat megtanulni, ehhez itt vagy itt is találhatsz segítséget.)

Mivel a szimmetria a tökéletes kiegyensúlyozottságot, a harmóniát sugalmazza, érthető, hogy általában népszerűbb az aszimmetriánál, amelyben mindig van feszültség, ám ettől még nem veszélyezteti a dolgok stabilitását. Érdekes módon ez a jellemzője gyakran még akkor is megmarad, amikor az emberi kapcsolatokban van jelen. Aszimmetrikusnak az a kapcsolatot nevezzük, amelyben például az egyik fél jobban szereti a másikat (tehát több érzelmet visz bele a kapcsolatba), ha mindenben az egyik a meghatározóbb, minden fontos kérdésben ő dönt, vagy ha minden elvégzendő munkát, a feladatokkal járó terhet mindig csak az egyik félnek kell viselnie. És bár az a gyakoribb, hogy ez végül a kapcsolat felbomlásához vezet, sokaknál mégis hosszú távon fennmaradhatnak az aszimmetrikus kapcsolatok. Például azért, mert sok ember számára kényelmesebb, ha nem neki kell döntenie, és mert azt szereti, ha irányítják. Mindenesetre az emberi kapcsolatok tere biztosan az egyetlen szféra, amelyben a szimmetria-aszimmetria konfliktusokat is okozhat – minden egyéb helyen egészen biztosan csupán a dolgok egymáshoz való viszonyának a speciális arányosságát jelenti.

Lévai Júlia